/ ML

Generative Model의 신흥강자, Diffusion Model!

이번 시간에 제가 소개해볼 논문이자 인공지능 모델은, 2021년 NeurIPS(신겅정보처리시스템학회) 에서 발표한 모델이자 생성모델 분야의 뜨거운 감자, Diffusion Model입니다! 이름이 왜 Diffusion Model인지, 모델 구조와 최적화 Metric을 유념하면서 AI 생성모델 분야에 어떠한 영향력을 미치고 있는지 한번 알아보도록 해요!

Generative Model?

  • 주어진 관측 데이터 x 로부터 추출된 분포(distribution)을 평가하는 모델! Autoregressive Model부터 VAE, GAN, Flow - Based Model 등 다양!

Diffusion model이어야 하는 이유?

  • 2021 NeurIPS 학회에서 Autoregressive 계열 생성모델보다 likelihood 성능이 좋고, GAN Based model보다 quality가 높은 sample 을 생성하는 것으로 발표되었답니다!
  • Diffusion Models Beat GANs on Image Synthesis

Diffusion Model

  • 점진적인 noise 추가의 역과정을 학습하는 것이 개념의 핵심
  • 주어진 데이터 x 로부터 noise를 추가하고, noise data로부터 x로 돌아오는 과정을 학습함
  • VAE와 컨셉은 유사하지만, data 분포를 학습하는 것이 아니라 Markov Chain 안에서 noise 분포를 모델링하는 Latent variable model
    • 여기서 markov chain이란, 특정한 확률적인 규칙에 의해 하나의 상태에서 다른 특정한 상태로 변화하는 수학적 계(界)를 의미함. 쉽게 말해, 확률에 의한 시간에 따른 상태 변화.
  • prior로부터 posterior를 얻기 위하여 x1,x2, xT 의 각 time point 별 latent varible에 noise를 더해가는 구조 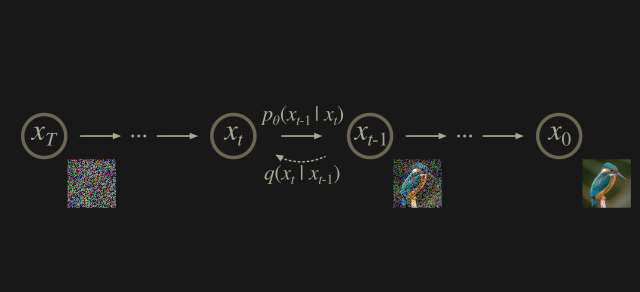noise를 추가하는 과정을 diffusion(확산 또는 전파)라고 이해할 수 있겠죠. $x_T$ 로부터 시간에 따라 조건부 확률에 의해 noise로부터 원래 이미지를 복원해나가는 모습입니다.
  • 계충적(hierachical)한 방법으로 data를 denoise, 다시 말해 decode를 하는 것이죠.

process

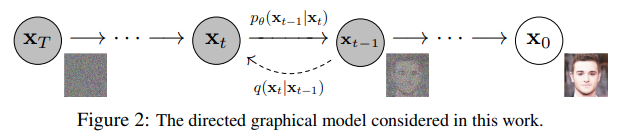
  • forward process
    • 점진적으로 noise를 더해가는 과정 $q$
    • real data의 distribution을 $q(x_0)$라고 한다면, sampling을 할 수 있음. ($x_0$ ~ $q(x_0)$)
      • time step 별로 gaussian noise를 추가하는 과정은 아래와 같다.

    • $q(x_t|x_{t-1}) = N(x_t ; \sqrt{1-\beta_t}x_{t-1}, \beta_tI)$

    • 여기서 $\beta$ 는 variance schedule(학습되기도 하고(parameter), 고정되기도 함(hyperparameter))이라고 해서, 직관적으로는 time step별로 추가될 noise의 분산에 해당하는 값이다.
    • diffusion model을 하나의 함수라고 한다면, model은 noisy component를 $\epsilon(x_t, t)$
      • true noise 와 predicted noise의 차이
  • reverse process
    • 학습된 denoising process $p_\theta$
    • 원래 $p(x_{t-1}|x_t)$ 의 conditional distribution에 가까운 $p_\theta(x_{t-1}|x_t)$ 를 학습하는 것!
      • 신경망이 위에 해당하는 parameter를 학습하고 loss 파악하고 gradient descent 로 update하는 과정!
    • 역과정도 Gaussian noise를 가정하므로, 정규분포의 평균과 분산이 parameter로 정의됨
      • $p_\theta(x_{t-1}|x_t) = N(x_{t_1}; \mu_\theta(x_t, t), \sigma_\theta(x_t, t))$
      • 허나 DDPM저자는 variance를 고정시키고, 조건부 확률 분포의 평균만 학습하게 함. 비슷한 결과를 보이기 때문. (이후 더 발전된 형태에서는 variance만 학습)
    • denoising 과정이 학습이 되어있음

반복 과정!

Benefits

  • scalability
  • parallelizabliity

objective function

negative log likelihood를 사용하며, 초기 이미지(ground truth)의 확률분포와 복원된 이미지의 확률분포 간 KL Divergence

  • 둘다 Gaussian distribution

각 time step의 Loss 를 모두 합한 것이 최종 loss가 됨

variance schedule이 학습 가능한 경우

각 time step의 loss 는 아래와 같이 정의되고,

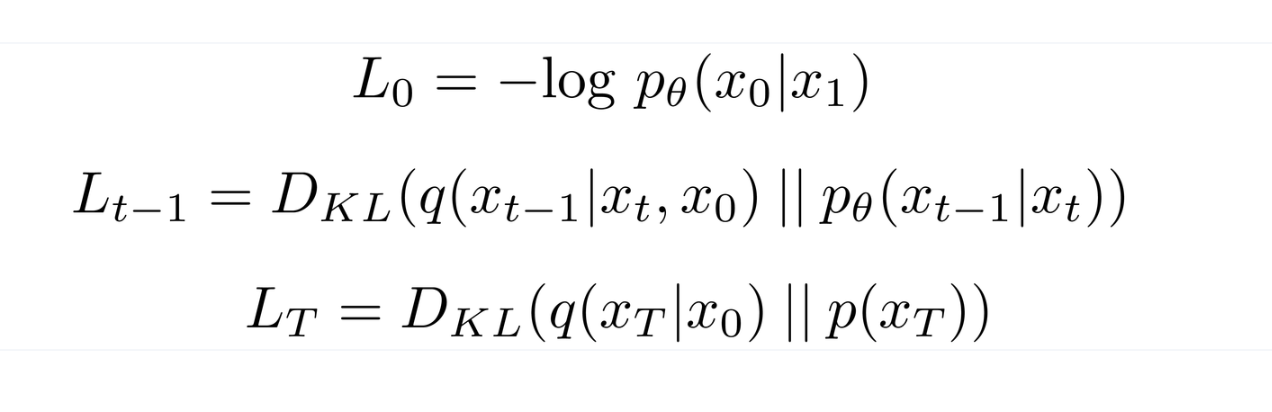
KL divergence?

  • 쉽게 이야기해서, 확률분포 간의 어긋난 정도

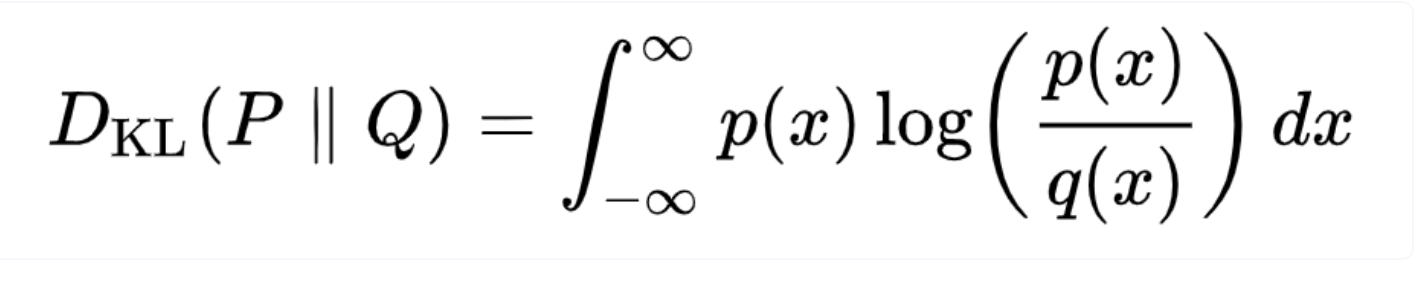
variance schedule을 고정시키면!

  • schedule을 고정시켜도 성능이 충분히 좋다
  • 선형 나열보다는 기하학적 나열이 더 성능이 좋음
  • $L_{t-1}$ = $|| \epsilon - \epsilon_\theta(x_t, t) ||^2$

정리 및 마무리

  • forward process에서 markov chain에 의한 gaussian noise를 추가하고, 특정 variance schedule을 따름
  • reverse process에서 parameter에 의해 원본 복원과정 학습
  • 모델 평가는, step별 loss의 합.
  • 특정 time step의 복원된 확률분포 $p$ 와 생성된 확률분포 $q$ 간의 차이를 비교함. KL Divregence 또는 gaussian distribution에 대응되는 noise간의 rmse score
  • 유연성이 좋고 다양한 모델에 적용 가능. 성능도 좋음 (ex, DALLE-2)

Reference

  • https://www.assemblyai.com/blog/diffusion-models-for-machine-learning-introduction/
  • https://arxiv.org/pdf/2006.11239.pdf
  • https://www.lgresearch.ai/kor/blog/view/?seq=190&page=1&pageSize=12